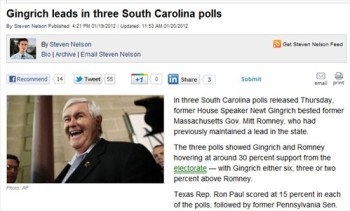
A screenshot from the Daily Caller's Jan. 19 post.

In a Jan. 19 article posted on Slate, Josh Voorhees summarizes the latest South Carolina poll results in these words:

“A new Rasmussen Reports poll shows Newt Gingrich leading Mitt Romney, 33-31, in the state (within the 4-point margin of error); an Insider Advantage poll has Newt up 32-29 (just within the 3.6-point margin of error); Public Policy Polling, which leans left, has Gingrich up 34-28 (outside of the 5-point MoE); Tarrance, which leans right, has Romney up 37-30 (outside of the 4.1-point MoE); and a Marist poll has Romney up 34-24 (outside of the 3.8-point MoE).”

I wrote to him, pointing out that he had erroneously characterized Gingrich’s lead over Romney in the Public Policy Polling (PPP) poll, and Romney’s leads over Gingrich in the Tarrance and Marist polls, as “outside” the margin of error. That would suggest that PPP’s poll showed Gingrich with a statistically significant lead over Romney, while Tarrance and Marist both showed Romney with a statistically significant lead over Gingrich.

In fact, the MoE of the percentage difference between the two candidates is roughly two times the poll’s stated MoE (it’s actually a little less than twice as large, but that rule of thumb provides a quick estimation).

That would mean that all five polls – including PPP, Tarrance, and Marist – showed leads that were all within the margins of error of the respective polls.

To his credit, Voorhees immediately wrote back, admitting the error and correcting the characterizations in his post. Unfortunately, his mistake is found quite often in many media reports of polls.

Look, for example, at the latest report from South Carolina: “Gingrich leads Clemson poll by 6 points” – 32 percent to 26 percent.

Or note the announcement from the Daily Caller: “Gingrich Leads in 3 South Carolina Polls.”  This announcement refers to polls by PPP (a 6-point lead for Gingrich), InsiderAdvantage (a 3-point advantage), and Rasmussen Reports (2-point lead).

Does Gingrich really lead among voters? The answer: No single poll can definitively say yes. Each shows a lead that is not outside the MoE of the respective poll.

A caveat: Doubling the MoE is only an approximation of the size of a lead a candidate needs to be “outside” the margin of error. There is a specific formula for calculating the MoE of the difference between two candidates, which pollsters typically do not provide. And it produces a result that is slightly less than double the poll’s maximum MoE.

The margin of error for the Clemson poll, for example, is 4.73 percentage points. If we double that figure, it is 9.46 percentage points, larger than Gingrich’s lead in the poll. His 6-point advantage in the poll is well within the poll’s MoE for the difference between Gingrich’s 32 percent and Romney’s 26 percent.

The problem is that the MoE applies to each percentage* – to the 32% figure and to the 26% figure.  That means Gingrich’s vote total is likely to be somewhere between 36.73% and 27.27% (32% plus or minus the 4.73 MoE), while Romney’s vote is likely to be somewhere between 30.73% and 21.27% (26% plus or minus 4.73 points).

So, in theory, according to the Clemson poll, it’s possible that Gingrich could lead by as much as 36.73% to 21.27% — almost a 16-point advantage. Or Romney could be up by 30.73% to 27.27% — almost a 4-point advantage.

The MoE tells us there is a 95% probability that the “true” figures are somewhere in-between those extremes.

Are polls really that imprecise?

Yes, indeed!

The PPP poll has a MoE of 5 points, which doubled is 10 points, clearly greater than PPP’s reported lead for Gingrich of 6 points. The other two polls – Insider Advantage and Rasmussen – both show leads so small (3 and 2 points respective), they’re both clearly too small to be statistically significant.

But as an approximation, multiplying the MoE by 2, and then seeing if it is at least as large as the difference between two candidates, is a quick and dirty way to see if a candidate is really leading another. (By “really” I mean there is a 95 percent probability that the difference between the two candidates is not due to chance.)

A final point worth noting: All the polls mentioned above showed Gingrich leading Romney, by an average of about 4 percentage points. The total sample size of all the polls is about 2,730 voters. Can we add them all together and calculate a MoE for all of them?

If all the polls were conducted in exactly the same way at the same time, using exactly the same methodology, it would be reasonable to do that. But given the different approaches, it’s a bit dicey to take all of the results and simply average them. But – if we did it anyway! – would the average difference of (roughly) 4.3 percentage points be statistically significant?

Maybe! I calculated the maximum MoE for that sample size at about 1.9 percentage points, assuming a perfectly random sample  – which typically is not the case. Often the pure MoE has to be multiplied by another factor, to account for different distortions in the process. The 4.3 average lead is larger than twice the MoE (3.8).

So, if the MoE is accurate, Gingrich’s lead is statistically significant.

In its final average, RealClearPolitics includes the latest Tarrance poll, the only one showing Romney ahead (by 7 points), along with the four polls just discussed (all showing Gingrich ahead). Thus, RCP’s average for Gingrich’s advantage is just 2.0 percentage points – within the MoE of all the polls combined.

So, will Gingrich win?

According to the polls, it’s too close to call!

Also, apart from the theoretical MoE, there is another real-world uncertainty – who will the undecided voters support? The undecided voters greatly outnumber the MoE, so the final outcome is anybody’s call.

We’ll find out soon.

*Actually, an MoE is calculated for each percentage, which varies by how close the percentage is to the 50 percent mark. The maximum MoE is when a percentage is exactly 50. By convention, pollsters announce that maximum MoE, which is used as an approximation of the MoE for each percentage reported in the study.

David W. Moore is a Senior Fellow with the Carsey Institute at the University of New Hampshire. He is a former Vice President of the Gallup Organization and was a senior editor with the Gallup Poll for thirteen years. He is author of The Opinion Makers: An Insider Exposes the Truth Behind the Polls (Beacon, 2008; trade paperback edition, 2009). Publishers’ Weekly refers to it as a “succinct and damning critique…Keen and witty throughout